Optionen an der Börse handeln - Wie schnell ändert sich der Preis einer Option (Gamma)
Einleitung
In den bisherigen Artikeln hast du die Faktoren kennengelernt, welche den Wert einer Option bestimmen:
- Delta als Kenngröße, wie stark der Optionspreis schwankt, wenn sich der Preis des zugrundeliegenden Basiswertes ändert
- Theta als Kenngröße, wie stark sich der Optionspreis im Laufe eines Tages verändert
- Vega als Kenngröße, wie stark sich der Optionspreis in Abhängigkeit von der impliziten Volatilität, also der erwarteten Schwankungsbreite des Basiswertes, ändert
In diesem Artikel lernst du mit Gamma (γ oder Γ) eine Kenngröße kennen, welche dir hilft, zu verstehen, wie schnell sich der Optionspreis in Abhängigkeit von Preisschwankungen des Basiswertes ändert. Oder einfach ausgedrückt, welche Auswirkungen Preisbewegungen des Basiswertes auf das Delta haben.
Definition und Erklärung
Das γ (Gamma) einer Option gibt an, wie schnell sich der Preis einer Option ändert, wenn sich der Wert des zugrundeliegenden Basiswertes um eine Geldeinheit ändert. Das γ gibt damit an, wie sich das δ (Delta) einer Option ändert, wenn sich der Preis des zugrundeliegenden Basiswertes um eine Geldeinheit ändert.
Da γ (GAMMA) beschreibt, welche Auswirkungen Schwankungen im Preis des Basiswertes auf das δ (DELTA) haben, gilt typischerweise für
- Put Optionen: 0 ≤ γ ≤ − δ und für
- Call Optionen: 0 ≥ − γ ≥ &delta .
Die liegt darin begründet, dass mit steigendem Preis des Basiswertes unter sonst gleichen Bedingungen das δ (DELTA) des Basiswertes für einen Put fällt, jedoch für einen Call steigt.
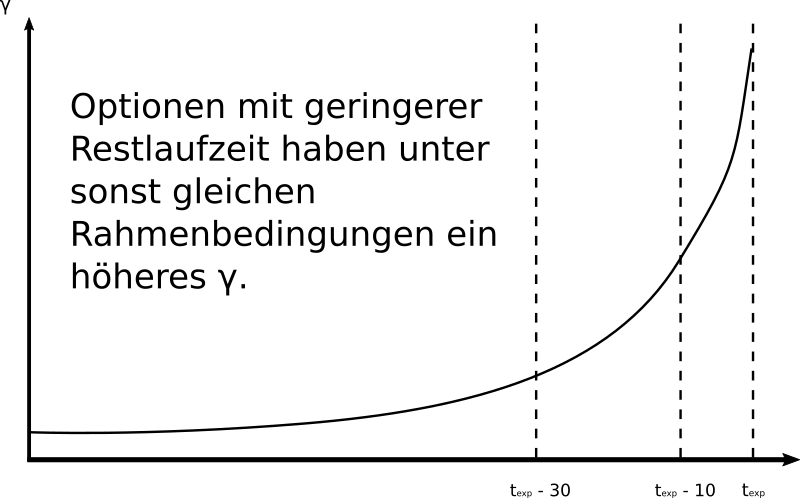 Der Verlauf von γ (Gamma) über die Laufzeit einer Option
Der Verlauf von γ (Gamma) über die Laufzeit einer Option
Dabei kann unter sonst gleichen Bedingungen (insb. gleiches δ und gleiches VEGA) beobachtet werden, dass bei Optionen mit geringerer Restlaufzeit das γ (GAMMA) höher ist, als bei Optionen mit längerer Restlaufzeit. Dies liegt darin begründet, dass Ausschläge im Preis des Basiswertes bei kurzer Restlaufzeit deutlich stärker ins Gewicht fallen, als wenn die Laufzeit der Option einen Ausgleich kurzfristiger Preisschwankungen des Basiswertes erlaubt.
Vergleichbar zum Zeitwertverfall einer Option, welcher durch das θ (THETA) abgebildet wird, steigt das γ (GAMMA) mit abnehmender Restlaufzeit einer Option an. Typische Schwellwerte in der Praxis, in denen die Auswirkungen des γ (GAMMA) überproportional steigen sind 30 Tage und 10 Tage Restlaufzeit.
Implikationen
Durch den erhöhten Anstieg von γ (GAMMA) in den letzten Tagen der Optionslaufzeit hat sich der Begriff der sogenannten Gamma-Woche etabliert. Insbesondere in der Gamma-Woche ist die Tendenz zu beobachten, dass es bei Optionen, bei denen der Preis des Basiswerts keinen hinreichen großen Abstand zum Strike aufweist, schon durch kleine Preisbewegungen des Basiswertes zu großen Preisbewegungen dieser Optionen führt. Eine gängige Methode zum Umgang mit diesem Umstand ist es, Optionen vor Verfall glattzustellen.
Disclaimer
Die in diesem Artikel enthaltenen Informationen dienen ausschließlich Ihrer Unterrichtung. Sie stellen keine Anlageberatung und keine steuerliche, rechtliche oder wirtschaftliche Beratung dar. Die in diesem Artikel bereitgestellten Informationen stellen keine Anlageberatung oder Anlageempfehlung dar und sind kein Angebot und keine Werbung zum Kauf oder Verkauf von Aktien oder Anteilen an einem in diesem Artikel genannten Finanzinstrument. Insbesondere ersetzen diese Informationen nicht eine geeignete anleger- und produktbezogene Beratung. Sofern nicht ausdrücklich anders angegeben, sind alle Preisinformationen unverbindlich und dienen ausschließlich der Illustration der verwendeten Beispiele. Sofern Sie Zweifel hinsichtlich der Bedeutung der in diesem Artikel bereitgestellten Informationen haben, wenden Sie sich bitte an Ihren Finanzberater, Steuerberater oder einen sonstigen unabhängigen, professionellen Berater.