Optionen an der Börse Handeln - der wichtigste Grieche - DELTA
Einleitung
In den letzten Artikeln hast du gelernt,
- was eine Option ist,
- wie sich der Wert einer Option bestimmen läßt,
- wann eine Option im Geld (in the money; ITM), am Geld (at the money; ATM) und aus dem Geld (out of the money; OTM) ist.
In diesem Artikel lernst du die vielleicht wichtigste Kennzahl im praktischen Umgang mit Optionen kennen. Das DELTA – δ oder Δ
Definition von DELTA und die Anwendung in der Praxis
DELTA ist einer der sogenannten Griechen (Greeks).
Die wichtigsten Options-Griechen (Greeks)
| Kennzahl |
Buchstabe |
Bedeutung |
| DELTA |
δ oder Δ |
Schwankungsanfälligkeit des Optionswertes bzgl. von Preisänderungen des Basiswertes |
| GAMMA |
γ oder Γ |
Schwankungsanfälligkeit des δ |
| THETA |
θ oder Θ |
Zeitwertverfall einer Option |
| VEGA |
ν oder κ, Κ |
Schwankungsanfälligkeit des Optionswertes bzgl. Änderungen der impliziten Volatilität |
DELTA läßt sich aus dem Black-Scholes Model herleiten und hat sich im praktischen Optionshandel als eine der wichtigsten Kenngrößen etabliert.
Definition
Je nach Quelle ist das DELTA mit unterschiedlichem Wortlaut, jedoch weitestgehend gleicher Bedeutung definiert. Eine geläufige Defintion wäre:
Das Delta gibt an, welche Auswirkungen eine Preisänderung des Basiswertes (Änderung des Aktienpreises) auf den Optionswert (Preis der Option) hat.
Anhand dieser Definition lassen sich mit Hilfe des Deltas drei für den Optionshandel relevante Fragen beantworten:
- Wie ändert sich der Optionspreis (Wert der Option) bei Änderungen des Aktienpreises?
- Wie vielen Aktien entspricht eine Option?
- Wie groß ist die Wahrscheinlichkeit, dass die Option zum Ende der Laufzeit im Geld (also in the money; ITM) ist?
Wie ändert sich der Optionswert bei Änderungen vom Aktienpreis?
Die Antwort auf die Frage, wie der Optionswert auf Änderungen des Aktienpreises reagiert, entspricht ziemlich präzise der Definition von Delta.
“Das Delta gibt, an, welche Auswirkung eine Preisänderungen des Basiswertes (Änderungen des Aktienpreises) auf den Optionswert (Preis der Option) hat.”
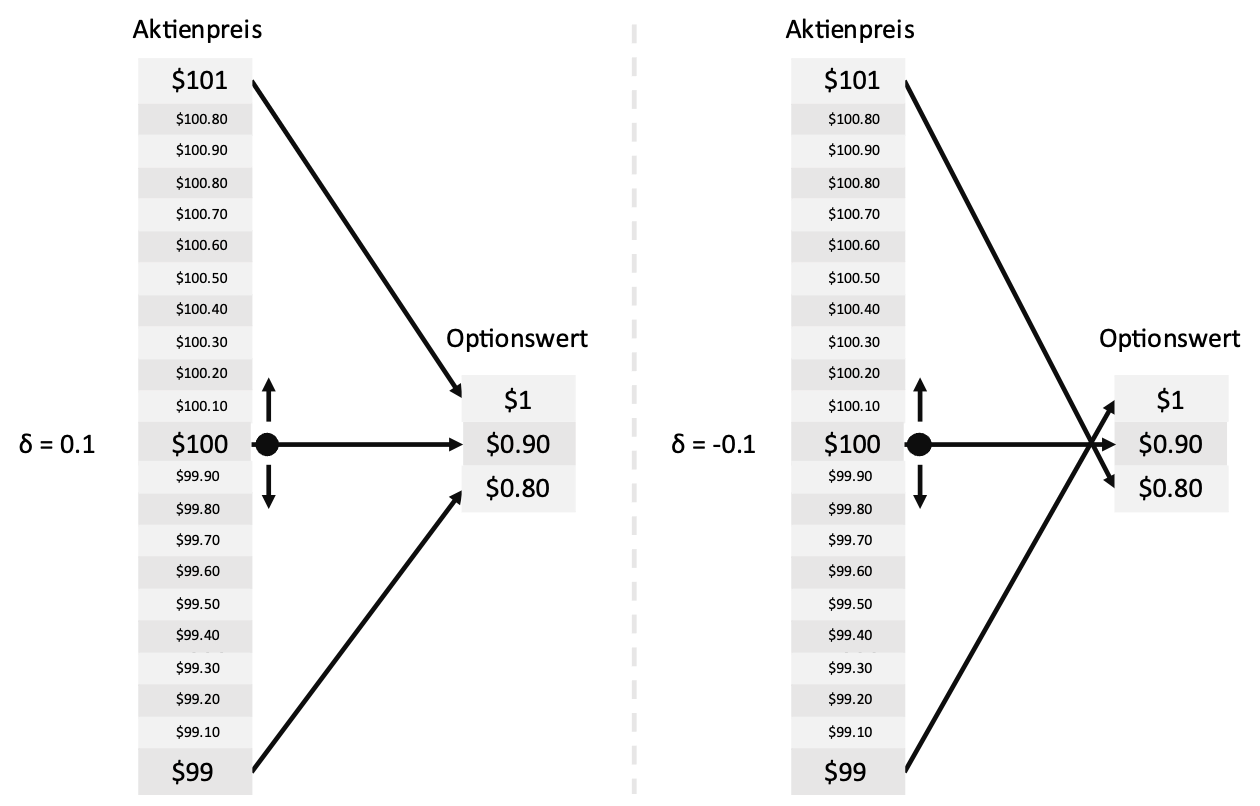 Auswirkungen von Änderungen im Aktienpreis auf den Optionswert bei δ = ± 0,1
Auswirkungen von Änderungen im Aktienpreis auf den Optionswert bei δ = ± 0,1
- Ein Delta von 0,1 sagt aus, dass der Preis der Option um 0,1 Geldeinheiten steigt, wenn der Aktienpreis um eine Geldeinheit steigt. Liegt der Optionswert also bei $0.90 und der Aktienpreis bei $100 würde der Optionswert auf $1 steigen, wenn der Aktienpreis auf $101 steigt. Sinkt der Aktienpreis hingegen auf $99 würde der Optionswert von $0.90 auf $0.80 sinken.
- Ein Delta von -0,1 sagt entsprechend aus, dass der Preis der Option um 0,1 Geldeinheiten sinkt, wenn der Aktienpreis um eine Geldeinheit steigt. Liegt der Optionswert also bei $0.90 und der Aktienpreis bei $100 würde der Optionswert auf $0.8 sinken, wenn der Aktienpreis auf $101 steigt. Sinkt der Aktienpreis hingegen auf $99 würde der Optionswert von $0.90 auf $1 steigen.
Auch wenn diese Interpretation am nächsten an der formalen Definition von DELTA liegt, ist sie dennoch vermutlich diejenige Interpretation mit der geringsten praktischen Relevanz für die meisten Optionshändler.
Allerdings läßt sich aus der Definition und dem Verständnis was eine Put Option ist, sehr intuitiv verstehen, dass Put Optionen immer ein negatives DELTA haben. Denn wenn der Aktienpreis steigt, sinkt die Wahrscheinlichkeit, dass die Put Option ins Geld läuft und entsprechend ist ein steigender Aktienpreis ein Auslöser für den Wertverfall von Put Optionen. Entsprechend ist das δ von Put Optionen immer negativ. Aus dem Verständnis, was eine Call Option ist, läßt sich ebenso intuitiv verstehen, dass Call Optionen immer ein positives DELTA haben. Denn wenn der Aktienpreis steigt, steigt die Wahrscheinlichkeit, dass die Call Option ins Geld läuft. Entsprechend ist ein steigender Aktienpreis ein Auslöser für Wertsteigerungen von Call Optionen.
Wichtig: Auch wenn das δ einer Call Option immer positiv ist und das δ einer Put Option immer negativ ist, heißt das nicht, dass der tatsächliche Optionswert sich bei Änderungen des Aktienpreises in die durch δ vorgegebenene Richtung bewegen muss. Dies liegt daran, dass der Aktienpreis nur einer der Einflussfaktoren auf den Optionswert ist. Wenn sich also andere Einflußfaktoren stärker auf den Wert der Option auswirken als der Aktienpreis, kann sich der Optionswert auch in die entgegengesetzte Richtung bewegen!
Wie vielen Aktien entspricht die Option ?
Eine praxisnähere Interpretation des DELTA ist es, DELTA als Kennzahl für die Anzahl an Aktien in einer wertmäßig vergleichbaren Aktienposition zu verstehen. Dieses Verständnis entspricht zwar nicht dem Wortlaut der Definition von DELTA, läßt sich jedoch sehr intuitiv aus dieser herleiten.
Wenn eine Option ein DELTA von z.B. 0,15 hat, so bedeutet dies, dass der Optionswert um 0,15 Geldeinheiten steigt, wenn der Aktienpreis um
eine Geldeinheit steigt.
Da sich ein Optionskontrakt auf 100 Aktien bezieht, entspricht eine Option mit DELTA 0,15 in ihrem Verhalten bzgl. der Wertänderung einer Positionsgröße von 15 Aktien.
Eine andere sehr vergleichbare Sichtweise dieser Interpretation ist die, dass das DELTA angibt, zu wieviel Prozent einer vergleichbaren Aktienposition sich der Optionsverkäufer dem Marktrisiko aussetzt. Ein DELTA von ± 0,15 kann entsprechend als eine 15% Exposition gegenüber dem Marktrisiko einer vergleichbaren Aktienposition verstanden werden.
Wichtig: Das Delta ist keine Konstante, sondern stetigen Änderungen unterworfen. Entsprechend sind alle Schlussfolgerungen aus Delta mehr als Momentaufnahme, denn als stabile Aussagen zu verstehen! Dies ist insbesondere bei Risikobetrachtungen von besonderer Bedeutung.
Wie groß ist die Wahrscheinlichkeit, dass die Option zum Verfallstag im Geld ist?
Neben der definitionsgemäßen Verwendung von DELTA , wie der Optionswert auf Änderungen im Preis des Basiswertes reagiert und der praxisorientierten Interpretation, wie vielen Aktien eine Option in ihrem Wertänderungsverhalten entspricht, läßt sich DELTA auch als Annäherung an die Wahrscheinlichkeit verwenden, dass die Option zum Verfallstag im Geld also In the Money (ITM) ist.
Das bedeutet für eine Option mit DELTA ± 0,15, dass etwa 15% eine sehr praxisnahe Annäherung an die Wahrscheinlichkeit ist, dass die Option zum Verfallstag im Geld ist.
Für eine Put Option also, dass der Aktienpreis unterhalb des Strikes liegt und für eine Call Option, dass der Aktienpreis oberhalb des Strikes liegt.
Die Verwendung von DELTA als Annäherung an die Wahrscheinlichkeit, dass die Option zum Verfallstag im Geld – also In the Money (ITM) – ist, ist durchaus gebräuchlich. Jedoch ist DELTA nur näherungsweise mit der mathematischen Wahrscheinlichkeit vergleichbar.
Wichtig: Insbesondere sind die Ereignisse, die zu Veränderungen von DELTA bei verschiedenen Aktien führen nicht zwingend unabhängig oder gar verschieden von einander sind. Daher sind Wahrscheinlichkeitsbetrachtungen für mehrere Wertpapiere auf Basis von DELTA alles andere als präzise und können zu groben Fehlinterpretationen führen.
Disclaimer
Die in diesem Artikel enthaltenen Informationen dienen ausschließlich Ihrer Unterrichtung. Sie stellen keine Anlageberatung und keine steuerliche, rechtliche oder wirtschaftliche Beratung dar. Die in diesem Artikel bereitgestellten Informationen stellen keine Anlageberatung oder Anlageempfehlung dar und sind kein Angebot und keine Werbung zum Kauf oder Verkauf von Aktien oder Anteilen an einem in diesem Artikel genannten Finanzinstrument. Insbesondere ersetzen diese Informationen nicht eine geeignete anleger- und produktbezogene Beratung. Sofern nicht ausdrücklich anders angegeben, sind alle Preisinformationen unverbindlich und dienen ausschließlich der Illustration der verwendeten Beispiele. Sofern Sie Zweifel hinsichtlich der Bedeutung der in diesem Artikel bereitgestellten Informationen haben, wenden Sie sich bitte an Ihren Finanzberater, Steuerberater oder einen sonstigen unabhängigen, professionellen Berater.